import numpy as np
import numpy.random
import matplotlib.pyplot as plt
# this is probably the default, but just in case
%matplotlib inlineCLASSIFICATION
Dot Product as a basis for classification
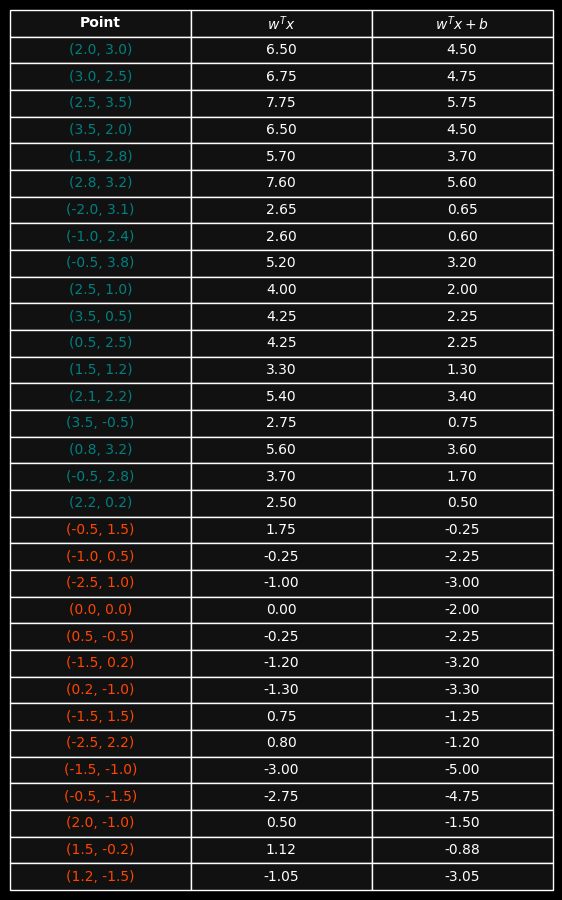
In the diagram below we plot a number of points from two different classes - one set are teal, one set are red. For simplicity they’re plotted such that all of the teal points lie on the right-hand side of the y-axis, while all of the red points lie on the left-hand side. In this example the vertical Y-Axis acts as a dividing line between these two classes of points - known as the decision boundary.The question is, if we have a set of points from different classes - is there a way to mathematically find a line tht divides them according to their class (assuming they are separable)?
# Example points: teal in Q1 & Q4 (x1>0), red in Q2 & Q3 (x1<0)
teal_pts = np.array([
[ 0.3, 3.2], # Q1 - POINT A
[1.5, 2.8],
[ 3.4, 2.6], # Q1
[ 1.0, -2.6], # Q4
[ 3.0, -1.0], # Q4
[0.5, 0.8],
[1.2, -1.4],
[2.7, 0.9],
[1.8, -0.3]
])
red_pts = np.array([
[-1.0, 2.0], # Q2 - POINT A
[-0.5, 3.0],
[-2.3, 1.5], # Q2
[-1.7, -1.2], # Q3
[-1.4, -2.2], # Q3
[-3.0, -1.0], # Q3
[-0.5, -3],
[-1.4, 0.5],
[-2.5, 2.8]
])
with plt.style.context("dark_background"):
fig, ax = plt.subplots(figsize=(6, 6))
# plot points
ax.scatter(teal_pts[:,0], teal_pts[:,1], s=35, color="teal", zorder=3)
ax.scatter(red_pts[:,0], red_pts[:,1], s=35, color="orangered", zorder=3)
# pot the axes + grid
ax.axhline(0, color="white", linewidth=2)
ax.axvline(0, color="white", linewidth=2)
ax.text(0.1, 3.6, r"decision boundary", color="white", fontsize=10)
ax.set_aspect("equal", adjustable="box")
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
ax.grid(True, alpha=0.3)
# add labels
ax.set_xlabel(r"$x_1$")
ax.set_ylabel(r"$x_2$")
ax.set_title(r"Various 2-dimensional points from two classes (red, teal)", fontsize="10")
plt.show()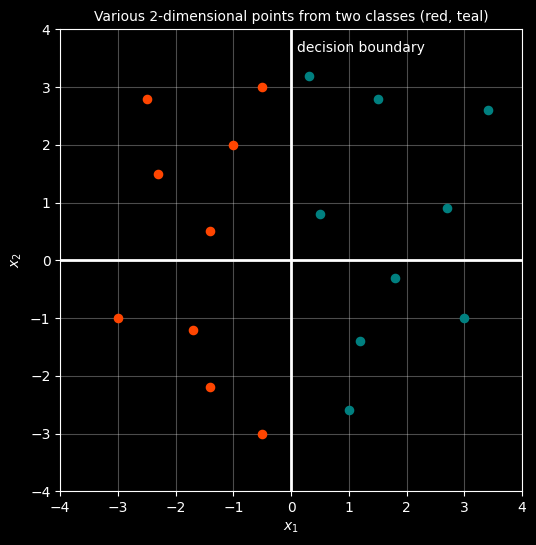
So in fact what a Machine Learning algorithm will do is try to find a weights vector, \(W\) which, when dotproduct with points of one class gives a positive result and a negative result against the other. The decision boundary is then the line perpendiculr to \(W\)!
#
# NOTE
# Run the previous cell first
#
show_vector_lines = True
show_dot_products = True
# identify a wieghts vecgor for illustration
w = np.array([1.5, 0.0])
with plt.style.context("dark_background"):
fig, ax = plt.subplots(figsize=(6, 6))
# plot points
ax.scatter(teal_pts[:,0], teal_pts[:,1], s=35, color="teal", zorder=3)
ax.scatter(red_pts[:,0], red_pts[:,1], s=35, color="orangered", zorder=3)
# axes + grid
ax.axhline(0, color="grey", linewidth=1)
ax.axvline(0, color="yellow", linewidth=2)
ax.text(0.1, 3.6, r"decision boundary", color="white", fontsize=10)
# arrows from origin to each point
if show_vector_lines:
for pt in teal_pts:
ax.arrow(0, 0, pt[0], pt[1], length_includes_head=True, head_width=0.12, head_length=0.2, linewidth=0.5, color="teal")
for pt in red_pts:
ax.arrow(0, 0, pt[0], pt[1], length_includes_head=True, head_width=0.12, head_length=0.2, linewidth=0.5, color="orangered")
# Weight vector (perpendicular to boundary)
ax.arrow(0, 0, w[0], w[1], length_includes_head=True, head_width=0.12, head_length=0.2, linewidth=2.5, color="fuchsia")
ax.text(1.5, 0.2, "w", color="fuchsia", fontsize=12)
# Compute dot product of each point with W, the vecror perpendicular to the Y-Axis decision boundary
if show_dot_products:
teal_scores = teal_pts @ w
red_scores = red_pts @ w
for x, s in zip(teal_pts, teal_scores):
ax.text(x[0] + 0.15, x[1] + 0.15, f"{s:.1f}", color="teal", fontsize=10)
for x, s in zip(red_pts, red_scores):
ax.text(x[0] + 0.15, x[1] + 0.15, f"{s:.1f}", color="orangered", fontsize=10)
ax.set_aspect("equal", adjustable="box")
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
ax.grid(True, alpha=0.3)
ax.set_xlabel(r"$x_1$")
ax.set_ylabel(r"$x_2$")
ax.set_title(r"Vectors for teal and red points and their dot product with W", fontsize="10")
plt.show()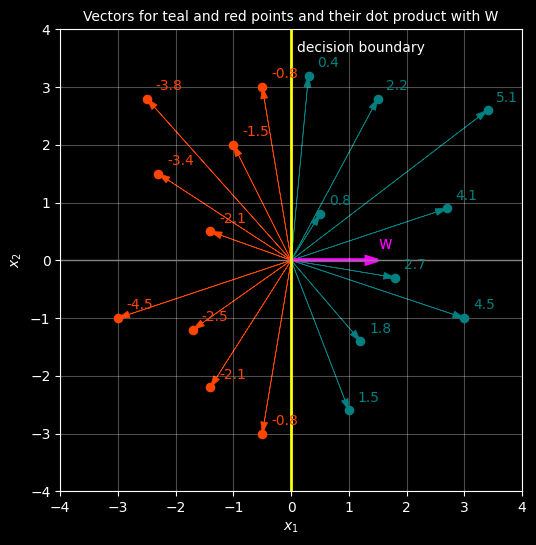
Perceptron Algorithm
The perceptron algorithm is a classic approach to finding a decision boundary on a set of points that are linearly separable. It works by starting with a weights vector and initiatlising it to [0,0], working out the dot products and scoring how many classificaitons it got incorrect. It then makes a change to the Weights vector and tries again. It keeps going until it successfully find a W that works and the decisoin boundary is then perpendicular to that W vector.Note that it may not choose the BEST solutoin, but if the points can be separated it is guaranteed to work.
import numpy as np
import matplotlib.pyplot as plt
# Data points
teal_pts = np.array([
[ 0.6, 3.2],
[1.5, 2.8],
[ 3.4, 2.6],
[ 1.0, -2.6],
[ 3.0, -1.0],
[0.5, 0.8],
[1.2, -1.4],
[2.7, 0.9],
[1.8, -0.3]
])
red_pts = np.array([
[-1.0, 2.0],
[-0.5, 3.0],
[-2.3, 1.5],
[-1.7, -1.2],
[-1.4, -2.2],
[-3.0, -1.0],
[-0.7, -3],
[-1.4, 0.5],
[-2.5, 2.8]
])
# Perceptron class
class Perceptron:
def __init__(self, learning_rate=0.1):
self.lr = learning_rate
self.w = np.random.randn(2) * 0.1 # Random initialization of W - hence you get different results each time
self.history = [self.w.copy()]
# calculate the dotproduct of the current W with the current point and
# return '1' for a positive result and '-1' for a negative result
def predict(self, x):
"""Return 1 if w^T x >= 0, else -1"""
dot_prod = np.dot(self.w, x)
return 1 if dot_prod >= 0 else -1
# training loop where we loop through each set of points and the labels provided (Y)
def train_epoch(self, X, y):
"""Train for one epoch, return number of misclassifications and details"""
mistakes = 0
mistake_details = []
all_predictions = []
for idx, (xi, yi) in enumerate(zip(X, y)):
dot_prod = np.dot(self.w, xi)
pred = self.predict(xi)
actual_label = "teal" if yi == 1 else "red"
pred_label = "teal" if pred == 1 else "red"
is_correct = pred == yi
all_predictions.append({
'idx': idx,
'point': xi,
'actual': actual_label,
'predicted': pred_label,
'dot_product': dot_prod,
'correct': is_correct
})
# this basically says that if the predicted label is not the same as the actual label in Y
# then tweak W
if not is_correct:
# Update: w = w + lr * yi * xi
self.w += self.lr * yi * xi
mistakes += 1
mistake_details.append(all_predictions[-1])
self.history.append(self.w.copy())
return mistakes, mistake_details, all_predictions
# Here we just convert our points into a matrix
X = np.vstack([teal_pts, red_pts])
# and rather than using colours to identyf classes we use number 1 for teal and -1 for red
y = np.hstack([np.ones(len(teal_pts)), -np.ones(len(red_pts))])
# Create an instance of the Perceptron class
perceptron = Perceptron(learning_rate=0.1)
mistakes_per_epoch = [0] # Initial state has 0 mistakes before training
# Now train on each point
for epoch in range(10): # Allow up to 10 iterations
mistakes, mistake_details, all_predictions = perceptron.train_epoch(X, y)
mistakes_per_epoch.append(mistakes)
print(f"\n{'='*70}")
print(f"EPOCH {epoch+1}")
print(f"{'='*70}")
print(f"Weight vector: w = {perceptron.w}")
print(f"Total misclassifications: {mistakes}\n")
# Show all predictions
print("All Predictions:")
print(f"{'Idx':<5} {'Point':<20} {'Actual':<10} {'Predicted':<10} {'Dot Prod':<12} {'Status':<10}")
print("-" * 70)
for pred in all_predictions:
status = "✓ CORRECT" if pred['correct'] else "✗ WRONG"
print(f"{pred['idx']:<5} {str(pred['point']):<20} {pred['actual']:<10} {pred['predicted']:<10} {pred['dot_product']:<12.3f} {status:<10}")
# Show misclassifications in detail
if mistake_details:
print(f"\nMisclassified points (that were corrected):")
print("-" * 70)
for detail in mistake_details:
print(f" Point {detail['idx']}: {detail['point']} -> "
f"Predicted {detail['predicted']}, but was actually {detail['actual']} "
f"(dot product: {detail['dot_product']:.3f})")
else:
print("\n✓ NO MISCLASSIFICATIONS - CONVERGED!")
if mistakes == 0:
print(f"\nConverged after {epoch+1} epochs!")
break
# Visualize iterations until convergence
num_iterations = len(perceptron.history)
cols = 5
rows = (num_iterations + cols - 1) // cols # Calculate rows needed
with plt.style.context("dark_background"):
fig, axes = plt.subplots(rows, cols, figsize=(14, 3*rows))
axes = axes.flatten()
for iteration, (w, mistakes) in enumerate(zip(perceptron.history, mistakes_per_epoch)):
ax = axes[iteration]
# Plot points
ax.scatter(teal_pts[:,0], teal_pts[:,1], s=25, color="teal", zorder=3)
ax.scatter(red_pts[:,0], red_pts[:,1], s=25, color="orangered", zorder=3)
# Decision boundary: w^T x = 0
x_range = np.linspace(-4, 4, 100)
if abs(w[1]) > 0.01: # w2 is not ~0
x2_boundary = -(w[0] / w[1]) * x_range
ax.plot(x_range, x2_boundary, color="yellow", linewidth=2)
else: # boundary is vertical
ax.axvline(0, color="yellow", linewidth=2)
# Weight vector
ax.arrow(0, 0, w[0], w[1],
length_includes_head=True,
head_width=0.12, head_length=0.2,
linewidth=2, color="fuchsia")
# Axes and grid
ax.axhline(0, color="grey", linewidth=1)
ax.axvline(0, color="grey", linewidth=1)
ax.set_aspect("equal", adjustable="box")
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
ax.grid(True, alpha=0.3)
ax.set_xlabel(r"$x_1$", fontsize=9)
ax.set_ylabel(r"$x_2$", fontsize=9)
ax.set_title(f"Iteration {iteration}: {mistakes} misclassifications", fontsize=10)
# Hide unused subplots
for idx in range(num_iterations, len(axes)):
axes[idx].set_visible(False)
plt.tight_layout()
plt.show()
print(f"\n{'='*70}")
print(f"Final weight vector: {perceptron.w}")
print(f"{'='*70}")
======================================================================
EPOCH 1
======================================================================
Weight vector: w = [0.17807853 0.01441715]
Total misclassifications: 2
All Predictions:
Idx Point Actual Predicted Dot Prod Status
----------------------------------------------------------------------
0 [0.6 3.2] teal red -0.135 ✗ WRONG
1 [1.5 2.8] teal teal 0.885 ✓ CORRECT
2 [3.4 2.6] teal teal 0.979 ✓ CORRECT
3 [ 1. -2.6] teal red -0.635 ✗ WRONG
4 [ 3. -1.] teal teal 0.520 ✓ CORRECT
5 [0.5 0.8] teal teal 0.101 ✓ CORRECT
6 [ 1.2 -1.4] teal teal 0.194 ✓ CORRECT
7 [2.7 0.9] teal teal 0.494 ✓ CORRECT
8 [ 1.8 -0.3] teal teal 0.316 ✓ CORRECT
9 [-1. 2.] red red -0.149 ✓ CORRECT
10 [-0.5 3. ] red red -0.046 ✓ CORRECT
11 [-2.3 1.5] red red -0.388 ✓ CORRECT
12 [-1.7 -1.2] red red -0.320 ✓ CORRECT
13 [-1.4 -2.2] red red -0.281 ✓ CORRECT
14 [-3. -1.] red red -0.549 ✓ CORRECT
15 [-0.7 -3. ] red red -0.168 ✓ CORRECT
16 [-1.4 0.5] red red -0.242 ✓ CORRECT
17 [-2.5 2.8] red red -0.405 ✓ CORRECT
Misclassified points (that were corrected):
----------------------------------------------------------------------
Point 0: [0.6 3.2] -> Predicted red, but was actually teal (dot product: -0.135)
Point 3: [ 1. -2.6] -> Predicted red, but was actually teal (dot product: -0.635)
======================================================================
EPOCH 2
======================================================================
Weight vector: w = [0.17807853 0.01441715]
Total misclassifications: 0
All Predictions:
Idx Point Actual Predicted Dot Prod Status
----------------------------------------------------------------------
0 [0.6 3.2] teal teal 0.153 ✓ CORRECT
1 [1.5 2.8] teal teal 0.307 ✓ CORRECT
2 [3.4 2.6] teal teal 0.643 ✓ CORRECT
3 [ 1. -2.6] teal teal 0.141 ✓ CORRECT
4 [ 3. -1.] teal teal 0.520 ✓ CORRECT
5 [0.5 0.8] teal teal 0.101 ✓ CORRECT
6 [ 1.2 -1.4] teal teal 0.194 ✓ CORRECT
7 [2.7 0.9] teal teal 0.494 ✓ CORRECT
8 [ 1.8 -0.3] teal teal 0.316 ✓ CORRECT
9 [-1. 2.] red red -0.149 ✓ CORRECT
10 [-0.5 3. ] red red -0.046 ✓ CORRECT
11 [-2.3 1.5] red red -0.388 ✓ CORRECT
12 [-1.7 -1.2] red red -0.320 ✓ CORRECT
13 [-1.4 -2.2] red red -0.281 ✓ CORRECT
14 [-3. -1.] red red -0.549 ✓ CORRECT
15 [-0.7 -3. ] red red -0.168 ✓ CORRECT
16 [-1.4 0.5] red red -0.242 ✓ CORRECT
17 [-2.5 2.8] red red -0.405 ✓ CORRECT
✓ NO MISCLASSIFICATIONS - CONVERGED!
Converged after 2 epochs!
======================================================================
Final weight vector: [0.17807853 0.01441715]
======================================================================# --- Final perceptron result (4x4, same style, with visual-only jitter) ---
import matplotlib.pyplot as plt
import numpy as np
w = perceptron.w # final weight vector
with plt.style.context("dark_background"):
fig, ax = plt.subplots(figsize=(4, 4))
# Points (jittered only for display)
ax.scatter(teal_plot[:, 0], teal_plot[:, 1], s=25, color="teal", zorder=3)
ax.scatter(red_plot[:, 0], red_plot[:, 1], s=25, color="orangered", zorder=3)
# Decision boundary: w^T x = 0
if abs(w[1]) > 0.01:
x = [-4, 4]
y = [-(w[0] / w[1]) * xi for xi in x]
ax.plot(x, y, color="yellow", linewidth=2)
else:
ax.axvline(0, color="yellow", linewidth=2)
# Weight vector
ax.arrow(
0, 0, w[0], w[1],
length_includes_head=True,
head_width=0.12, head_length=0.2,
linewidth=2, color="fuchsia"
)
# Axes & grid
ax.axhline(0, color="grey", linewidth=1)
ax.axvline(0, color="grey", linewidth=1)
ax.set_aspect("equal", adjustable="box")
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
ax.grid(True, alpha=0.3)
ax.set_xlabel(r"$x_1$", fontsize=9)
ax.set_ylabel(r"$x_2$", fontsize=9)
# Title
ax.set_title("Final Perceptron Decision Boundary", fontsize=10)
# Final parameters inside the plot
ax.text(
-3.8, 3.6,
rf"$\mathbf{{w}} = [{w[0]:.3f},\ {w[1]:.3f}]$",
fontsize=9,
color="white"
)
plt.show()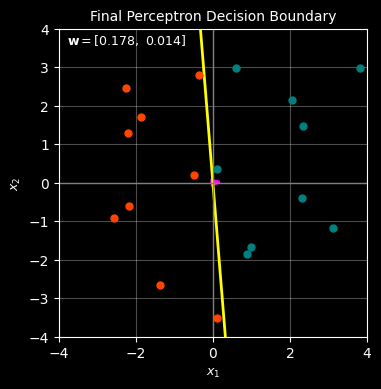
A more complex example
# CONFIG
show_decision_boundary = True
show_vector_lines = True
show_dot_products = False
show_bias = True # NEW CONFIG
# Weight vector and bias for tilted boundary
w = np.array([1.0, 1.5])
b = -2.0 # bias: decision boundary is w^T x + b = 0
# More points: teal above/right of boundary, red below/left
teal_pts = np.array([
[ 2.0, 3.0],
[ 3.0, 2.5],
[ 2.5, 3.5],
[ 3.5, 2.0],
[ 1.5, 2.8],
[ 2.8, 3.2],
[-2, 3.1],
[-1, 2.4],
[-0.5, 3.8],
[2.5, 1.0],
[3.5, 0.5],
[0.5, 2.5],
[1.5, 1.2],
[2.1, 2.2],
[3.5, -0.5],
[0.8, 3.2],
[-0.5, 2.8],
[2.2, 0.2]
])
red_pts = np.array([
[-0.5, 1.5],
[-1.0, 0.5],
[-2.5, 1.0],
[ 0.5, -0.5],
[-1.5, 0.2],
[ 0.2, -1.0],
[-1.5, 1.5],
[-2.5, 2.2],
[-1.5, -1],
[-0.5, -1.5],
[2,-1],
[1.5, -.25],
[1.2, -1.5],
])
# Compute dot products
teal_scores = teal_pts @ w + b
red_scores = red_pts @ w + b
with plt.style.context("dark_background"):
fig, ax = plt.subplots(figsize=(6, 6))
# plot points
ax.scatter(teal_pts[:,0], teal_pts[:,1], s=35, color="teal", zorder=3)
ax.scatter(red_pts[:,0], red_pts[:,1], s=35, color="orangered", zorder=3)
# arrows from origin to each point
if show_vector_lines:
for pt in teal_pts:
ax.arrow(0, 0, pt[0], pt[1], length_includes_head=True, head_width=0.12, head_length=0.2, linewidth=0.5, color="teal")
for pt in red_pts:
ax.arrow(0, 0, pt[0], pt[1], length_includes_head=True, head_width=0.12, head_length=0.2, linewidth=0.5, color="orangered")
# axes + grid
ax.axhline(0, color="lightgray", linewidth=1)
ax.axvline(0, color="lightgray", linewidth=1)
if show_decision_boundary:
# Decision boundary: w^T x + b = 0 => x2 = -(w[0]*x1 + b) / w[1]
x1_range = np.linspace(-3, 4, 100)
x2_boundary = -(w[0] * x1_range + b) / w[1]
ax.plot(x1_range, x2_boundary, color="deepskyblue", linewidth=2)
# Weight vector (perpendicular to boundary)
ax.arrow(0, 0, w[0], w[1],
length_includes_head=True,
head_width=0.12, head_length=0.2,
linewidth=2, color="fuchsia")
ax.text(w[0] - 0.2, w[1] + 0.2, "w", color="fuchsia", fontsize=12)
# annotate scores
if show_dot_products:
for x, s in zip(teal_pts, teal_scores):
ax.text(x[0] + 0.15, x[1] + 0.15, f"{s:.1f}", color="teal", fontsize=10)
for x, s in zip(red_pts, red_scores):
ax.text(x[0] + 0.15, x[1] + 0.15, f"{s:.1f}", color="orangered", fontsize=10)
ax.set_aspect("equal", adjustable="box")
ax.set_xlim(-3, 4)
ax.set_ylim(-2, 4)
ax.grid(True, alpha=0.3)
ax.set_xlabel(r"$x_1$")
ax.set_ylabel(r"$x_2$")
ax.set_title(r"Classification with offset decision boundary", fontsize="10")
plt.show()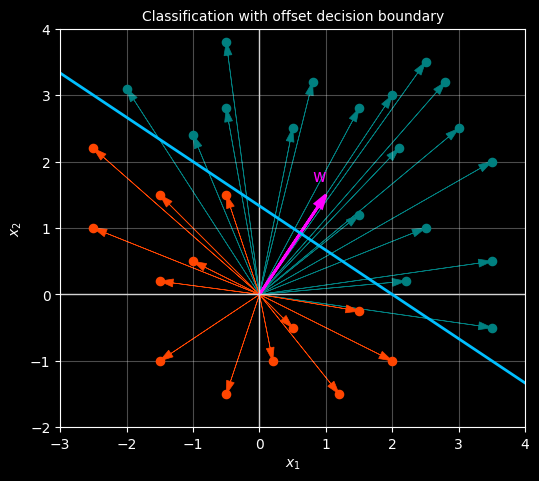
# Create table data
all_pts = np.vstack([teal_pts, red_pts])
all_colors = ['teal'] * len(teal_pts) + ['orangered'] * len(red_pts)
all_scores_w = all_pts @ w
all_scores_w_b = all_pts @ w + b
# Prepare table data
table_data = []
colors = []
for i, (pt, color) in enumerate(zip(all_pts, all_colors)):
table_data.append([
f"({pt[0]:.1f}, {pt[1]:.1f})",
f"{all_scores_w[i]:.2f}",
f"{all_scores_w_b[i]:.2f}"
])
colors.append(color)
# Create table
with plt.style.context("dark_background"):
fig, ax = plt.subplots(figsize=(7, 8))
ax.axis("off")
table = ax.table(
cellText=table_data,
colLabels=["Point", r"$w^T x$", r"$w^T x + b$"],
cellLoc="center",
colLoc="center",
loc="center"
)
table.auto_set_font_size(False)
table.set_fontsize(10)
table.scale(1.0, 1.6)
# Style cells
for (row, col), cell in table.get_celld().items():
cell.set_edgecolor("white")
cell.set_linewidth(1.0)
cell.set_facecolor("#111111")
# Header row
if row == 0:
cell.get_text().set_color("white")
cell.get_text().set_fontweight("bold")
# First column: colour matches point colour
elif col == 0:
cell.get_text().set_color(colors[row - 1])
# Other columns
else:
cell.get_text().set_color("white")
plt.show()